FOURIER
ET LES DESSINS
FOURIER ET LES DESSINS
Dessinez ce que vous souhaitez sur cette page, un dessin d’une seule ligne où la fin rejoint le début, par exemple une étoile…

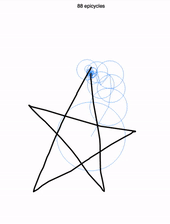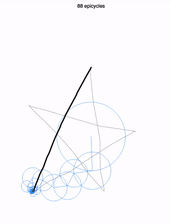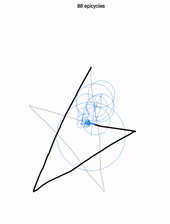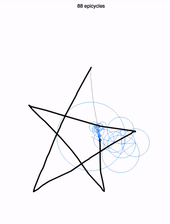
Aussitôt, un ensemble de cercles tournoyant apparaît, balayant votre dessin. Regardez attentivement. Chaque cercle tourne autour d’un cercle, lui même tournant autour d’un cercle… jusqu’à un premier cercle, immobile. À l’extrémité du dernier cercle, tout petit, un crayon imaginaire reproduit parfaitement votre dessin !

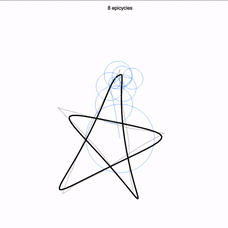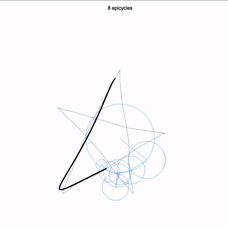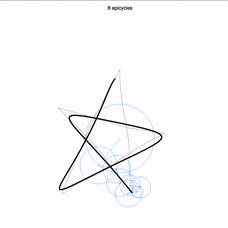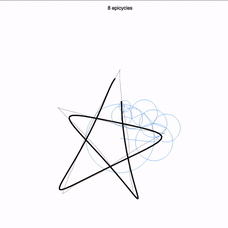
Plus impressionnant encore, vous pouvez, à l’aide d’un curseur au bas de l’écran, réduire le nombre de cercles utilisés (ici 88). Voici le dessin obtenu en ne gardant que les 8 premiers cercles !
Incroyable mais vrai : avec des cercles qui tournent autour de cercles qui tournent autour de cercles…, il est possible de s’approcher autant que l’on veut de n’importe quel dessin ! Pour reprendre les termes utilisés dans l’introduction : les cercles sont les éléments simples, la base permettant de reproduire n’importe quelle courbe fermée. À disposition, toutes les vitesses de rotations possible à partir d’une vitesse de base : 2 fois plus vite, 3 fois plus vite… et également dans l’autre sens. La seule chose qui varie pour s’approcher de l’un ou l’autre des dessins, c’est la taille de chacun de ces cercles, et la position d’origine des uns par rapport aux autres !
Le fait de pouvoir, la plupart du temps, réduire considérablement le nombre de cercles utilisés tout en conservant schématiquement le dessin montre immédiatement l’intérêt que peut avoir l’analyse de Fourier en terme de compression, même si ce n’est jamais sous cette forme qu’elle est utilisée (voir plutôt la section “photos” pour cet aspect)
De même, on peut remarquer qu’une image “simplifiée” est bien souvent également plus “lisse”. Le fait d’enlever les détails peut en réalité enlever les défauts d’une image ou d’un son (ici, les défauts sont dus à notre main qui tremble !)
Questions, défis : Est-il possible de faire d’autres “jolis ” dessins (comme l’étoile) qui peuvent être reproduits assez fidèlement avec un nombre très petit de cercles ? Et à l’inverse, quels dessins sont les plus difficiles à approcher par des cercles qui tournent ? Pourquoi ?

Pour aller plus loin, un site très riche : https://www.jezzamon.com/fourier/fr.html
